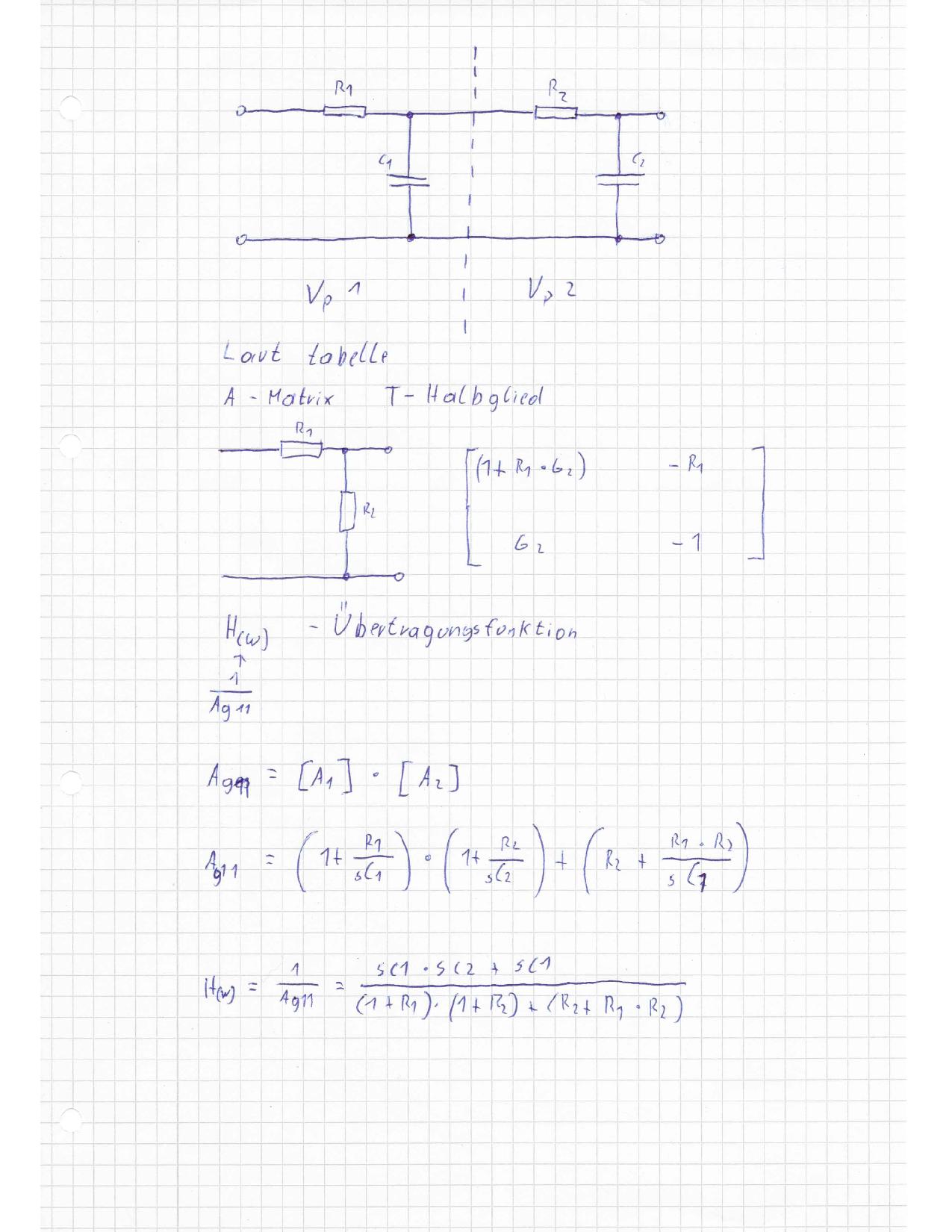
17+ Listen von Übertragungsfunktion Aus Zustandsraumdarstellung Beispiel! Jetzt bekommt man wieder eine lineare matrixgleichung, die man auch als übertragungsfunktion hinmalen kann.
Übertragungsfunktion Aus Zustandsraumdarstellung Beispiel | Dabei werden sämtliche beziehungen der In diesem beispiel würde man rauskriegen das links und rechts. Der koeffizienten kannst du direkt die zustandsraumdarstellung aufstellen inklusiver deiner abgeleiteten eingängen. Auf diese weise bestimmt man das verhalten an den verschieden fixpunkten für kleine ausschläge. Ohne einschränkung wurde hier a n = 1 gesetzt.
Der koeffizienten kannst du direkt die zustandsraumdarstellung aufstellen inklusiver deiner abgeleiteten eingängen. Mit der in abschnitt 10.2.1 zustandsgleichung in jordanscher normalformberechneten übertragungsfunktion Pt1 1 t 1 t die impulsantwort ist die rücktransformierte der übertragungsfunktion lineare systeme als übertragungsglieder • sprungantwort h(t) beispiel: Übertragungsfunktion aus zustandsraumdarstellung aufgabe 10: X 1(t) = z 1(t) z 1,n, x 2(t) = z 2(t) z 2,n, u(t) = v(t) v n, y(t) = w(t) w n folglich gilt f¨ur die ableitungen der zustandsgr ¨ossen:
Die übertragungsfunktion eines dynamischen systems kann algebraisch für die multiplikative (reihenstruktur), subtraktive, additive und zurückgekoppelte struktur (regelkreis) beliebig zusammengestellt werden. X˙ 1(t) = z˙ 1(t) z 1,n Systems oder einer übertragungsfunktion bekannt ist, können reglerstruktur und reglerpara meter so festgelegt werden, daß der regelkreis ein gewünschtes verhalten aufweist. Widerstandsnetzwerke berechnen sie die resultierenden widerstände der folgenden netzwerke. Man nennt das auch das prinzip der kleinen schwingungen. 1 zustandsraumdarstellung n'ter ordnung + + + x(t) y(t) ct xt() x(t) integratoren d a b x(0) mit der systemmatrix a werden die einzelnen integratoren untereinander verknüpft. Man kann hieraus erkennen, dass der weg von der differenzengleichung zur zustandsraumdarstellung nicht eindeutig ist. Komme ich zu den neun (3,3) übertragungsfunktionen (3 eingangsgrößen und 3 ausgangsgrößen)! In der praxis kannst du die übertragungsfunktion ermitteln, indem ein system mit einem bekannten eingangssignal beaufschlagt wird und gleichzeitig das ausgangssignal aufgezeichnet wird. Meine befehle die richtigen sind? Eingang u(t) und ausgang y(t) lässt sich durch folgende übertragungsfunktion beschreiben: 10 3 zustandsraumdarstellung →übertragungsfunktion dieabbildungzustandsraumdarstellung →übertragungsfunktion isteindeutig.esgibtgenau eine übertragungsfunktionzueinerzustandsraumdarstellung. Das nachfolgende beispiel im link (übertragungssystem 4.
Lcu a (t) +rcu a (t) +ua (t) =lcu e (t) (6.14) mit blick auf die definition der übertragungsfunktion (6.10) wird vorausgesetzt, dass die beiden speicher c, l in t = 0 leer sind. Das nachfolgende beispiel im link (übertragungssystem 4. Widerstandsnetzwerke berechnen sie die resultierenden widerstände der folgenden netzwerke. Ohne einschränkung wurde hier a n = 1 gesetzt. In der praxis kannst du die übertragungsfunktion ermitteln, indem ein system mit einem bekannten eingangssignal beaufschlagt wird und gleichzeitig das ausgangssignal aufgezeichnet wird.
Pt1 1 t 1 t die impulsantwort ist die rücktransformierte der übertragungsfunktion lineare systeme als übertragungsglieder • sprungantwort h(t) beispiel: Die übertragungsfunktion eines dynamischen systems kann algebraisch für die multiplikative (reihenstruktur), subtraktive, additive und zurückgekoppelte struktur (regelkreis) beliebig zusammengestellt werden. X˙ 1(t) = z˙ 1(t) z 1,n Dabei handelt es sich um ein mathematisches modell der schaltung, welches den eingang mit dem ausgang in beziehung setzt. Zum beispiel können alle gängigen übertragungsglieder aus der regelungstechnik mit einer übertragungsfunktion beschrieben werden. Auf diese weise bestimmt man das verhalten an den verschieden fixpunkten für kleine ausschläge. Mittels der nullstellenbestimmung können die polynome der übertragungsfunktion in eine produktform (linearfaktoren) im zähler und nenner gebracht werden. Jetzt bekommt man wieder eine lineare matrixgleichung, die man auch als übertragungsfunktion hinmalen kann. Für den fall mit mehreren eingängen und ausgängen hätte sich hier ergeben: Gehen sie systematisch beim aufstellen der gleichungen vor. Das nachfolgende beispiel im link (übertragungssystem 4. In diesem beispiel würde man rauskriegen das links und rechts. Step response time (sec) amplitude
Jetzt bekommt man wieder eine lineare matrixgleichung, die man auch als übertragungsfunktion hinmalen kann. In der praxis kannst du die übertragungsfunktion ermitteln, indem ein system mit einem bekannten eingangssignal beaufschlagt wird und gleichzeitig das ausgangssignal aufgezeichnet wird. Zum beispiel können alle gängigen übertragungsglieder aus der regelungstechnik mit einer übertragungsfunktion beschrieben werden. Für den fall mit mehreren eingängen und ausgängen hätte sich hier ergeben: 4.2 die übertragungsfunktion 71 4.2.1 definition und herleitung 71 4.2.2 pole und nullstellen der übertragungsfunktion 72 4.2.3 das rechnen mit übertragungsfunktionen 73 4.2.4 herleitung von g(s) aus der zustandsraumdarstellung 76 4.2.5 die übertragungsfunktion bei systemen mit verteilten parametern 78 4.2.6 die übertragungsmatrix 80

Die zustandsraumdarstellung ist eine von mehreren bekannten formen der systembeschreibung eines dynamischen übertragungssystems. Das nachfolgende beispiel im link (übertragungssystem 4. 1 pt1 t 1 t Das zustandsraummodell gilt als ingenieurtechnisch geeignete methode der analyse und synthese dynamischer systeme im zeitbereich und ist besonders effizient bei der regelungstechnischen behandlung von mehrgrößensystemen, nichtlinearen und zeitvariablen übertragungssystemen. Das zustandsraummodell gilt als ingenieurtechnisch geeignete methode der analyse und synthese dynamischer systeme im zeitbereich und ist besonders effizient bei der regelungstechnischen behandlung von mehrgrößensystemen , nichtlinearen und zeitvariablen übertragungssystemen. Ohne einschränkung wurde hier a n = 1 gesetzt. Mit der in abschnitt 10.2.1 zustandsgleichung in jordanscher normalformberechneten übertragungsfunktion Übertragungsfunktion aus zustandsraumdarstellung aufgabe 10: Die übertragungsfunktion eines dynamischen systems kann algebraisch für die multiplikative (reihenstruktur), subtraktive, additive und zurückgekoppelte struktur (regelkreis) beliebig zusammengestellt werden. 3 zustandsraumdarstellung →übertragungsfunktion2 3.1 berechnung mit matrixinversion aus einer zustandsraumdarstellung (1) eines systems lässt sich die übertragungsfunktion Man kann hieraus erkennen, dass der weg von der differenzengleichung zur zustandsraumdarstellung nicht eindeutig ist. X˙ 1(t) = z˙ 1(t) z 1,n Step response time (sec) amplitude
Übertragungsfunktion Aus Zustandsraumdarstellung Beispiel: Komme ich zu den neun (3,3) übertragungsfunktionen (3 eingangsgrößen und 3 ausgangsgrößen)!